Large language models (LLMs) learn in a remarkably simple way: by predicting the next token in a sequence. During pre-training, they process vast corpora and adjust parameters $\theta$ so that the probability assigned to the correct next token,

\[p_\theta(x_t \mid x_{<t}),\]

steadily rises. This is the familiar cross-entropy language-modeling objective.

At a high level, an LLM learns a map from context, what has already been seen, to expectation, a distribution for what should come next,. Fine-tuning, or post-training, refines this map for specific tasks: multi-step reasoning, following instructions, calibration, and so on.

A by-now standard empirical observation is that prompting models to produce Chain-of-Thought (CoT), step-by-step intermediate explanations, often yields striking improvements on reasoning tasks^[1]. Appending "Let’s think step by step" induces the model to unfold a short sequence of intermediate tokens that articulate a path:

"To solve this, first note the number is even; therefore dividing by two gives..."

Why should such intermediate text help?

An Information-Theoretic Perspective

Next-token prediction can be viewed as an exercise in uncertainty management. The surprisal of a token $x_t$ given its context $x_{<t}$ is

\[\text{surp}(x_t \mid x_{<t}) \;=\; -\log p_\theta(x_t \mid x_{<t}),\]

measured in bits. Surprisal counts how many “yes/no” questions one would need, on average, to identify the correct token under the model’s own distribution. High surprisal signals a difficult prediction (the model did not expect this token); low surprisal signals an easy one.

When a question is hard, we rarely vault straight to the answer. We instead lay down stepping stones: small statements that are easy to verify, each making the next step easier. CoT plays the same role for a model. Rather than a single long, unlikely jump $q \to a$, we nudge the model to traverse a short path

\[q \;\to\; r_1 \;\to\; r_2 \;\to\; \cdots \;\to\; r_k \;\to\; a,\]

so that each conditional $p_\theta(r_i \mid q, r_{<i})$ and $p_\theta(a \mid q, r_{1:k})$ is higher than it would have been without the preceding scaffolding. The informational load that would otherwise concentrate in a single cliff-edge step becomes distributed across the sentence in several gentler slopes.

Chain-of-Thought and Post Training Gradients

One can think of post-training not as the acquisition of new facts, but as the adjustment of geometry within a model that already knows much. Because language models are optimized under a cross-entropy objective, surprisal and gradient behavior are intimately linked: when the model’s predictions are more evenly distributed, its updates become steadier. Fine-tuning on Chain-of-Thought prompt-answer pairs achieves precisely this effect. The reasoning prefix redistributes surprisal across tokens, smoothing the loss surface and dampening abrupt fluctuations in the gradient with respect to the logits, what we may call gradient spikes. In essence, CoT supervision transforms learning from a sequence of sharp corrections into a flow of gentle, coherent updates.

Proof. Write $Z = \sum_j e^{x_j}$ and $p_i = e^{x_i}/Z$. Let $q$ denote the one-hot distribution from the training sample and $p_k$ represent the probability of predicting token $x_k$ from context $y_{<t}$.

For each $i$,

\[\log p_i = x_i - \log Z,\]

so

\[\frac{\partial}{\partial x_k} \log p_i = \frac{\partial x_i}{\partial x_k} - \frac{\partial \log Z}{\partial x_k} = \mathbb{I}\{i = k\} - \frac{1}{Z} \frac{\partial Z}{\partial x_k}\]

\[= \mathbb{I}\{i = k\} - \frac{e^{x_k}}{Z} = \mathbb{I}\{i = k\} - p_k.\]

Therefore,

\[\frac{\partial \mathcal{L}}{\partial x_k} = -\sum_{i=1}^V q(x_i) \frac{\partial}{\partial x_k} \log p_i = -\sum_i q(x_i)\bigl(\mathbb{I}\{i = k\} - p_k\bigr)\]

\[= -q(x_k) + p_k \sum_i q(x_i) = p_k - q(x_k),\]

since $\sum_i q(i) = 1$.

Specializing to the one-hot case $q = \mathbb{I}\{x_k = y_t\}$ gives

\[\frac{\partial \mathcal{L}}{\partial x_k} = p_k - \mathbb{I}\{x_k = y_t\},\]

as claimed. $\square$

We now use this to connect the size of the gradient to the model’s probability distribution.

Proof. Let $p$ denote the probability vector $p_\theta(\cdot \mid y_{<t})$ and $p_y$ represent $p_\theta(y_t \mid y_{<t})$. From Lemma 1, the gradient with respect to the logits satisfies

\[\|g\|^2 = (1 - p_y)^2 + \sum_{x_i \neq y_t} p_\theta(x_i \mid y_{<t})^2.\]

Rewriting,

\[\|g\|^2 = \|p\|_2^2 - 2p_y + 1.\]

Since the entries of $p$ are nonnegative and sum to one,

\[\|p\|_2^2 \leq p_y^2 + (1 - p_y)^2.\]

Substituting this bound gives

\[\|g\|^2 \leq 2(1 - p_y)^2.\]

Hence, if $|g| > \tau$, it follows that

\[p_y < 1 - \sqrt{\tfrac{\tau}{2}},\]

Similarly, we can use the bound

\[|p\|_2^2 \geq p_y^2\]

to get that

\[p_y > 1 - \sqrt{\tau}. \square\]

The magnitude of the gradient spike during training is thus largely governed by the tail of the model’s probability distribution: when the model assigns high probability to the correct token, the gradient necessarily remains small. Reasoning trace data is easier for the model to predict, effectively shifting the distribution of the correct token forward, moving the tail upwards and thereby reducing the frequency and severity of large gradients in practice.

Of course, if we used only the preceding lemma, one could only guarantee this in theory when the shift in probability exceeds roughly $\sqrt{\tau_{\text{direct}}}(1 - \sqrt{2}/2)$ in factor; the verification of this is left as an exercise to the reader. However, the inequalities employed above are somewhat generous, and in most realistic settings the stability improvement from CoT training probably appears far stronger than this conservative bound would suggest.

Empirical Results

Despite several attempts, I was not able to extend this proof to the model parameters without running into messy details with attention Jacobians. So, to give some empirical footing, I carried out a small experiment on Llama-3.1-8B-Instruct, using the GSM8K dataset as a simple and interpretable test bed.

The model was fine-tuned with full parameter updates using a batch size of 4, a learning rate of $1 \times 10^{-5}$, and a random seed of 42 across all runs. Since most instruction-tuned models already display some latent reasoning behavior when prompted, the goal was not to introduce reasoning, but to vary the degree to which it is supervised.

Instead of training solely on final answers, two supervision regimes were used:

• Direct: half of the reasoning steps in each explanation were randomly removed from the sample, leaving the remaining steps (and the final answer) supervised.
• Full-CoT: all reasoning and answer tokens were included in the training objective.

Each model was trained for 1000 optimizer steps, sufficient to observe early-phase dynamics where most geometric effects. During training, the following quantities were logged:

• Gradient norms (to track spike frequency and stability),
• Training loss (for convergence smoothness),
• Cosine similarity between consecutive gradients (to measure local coherence), and
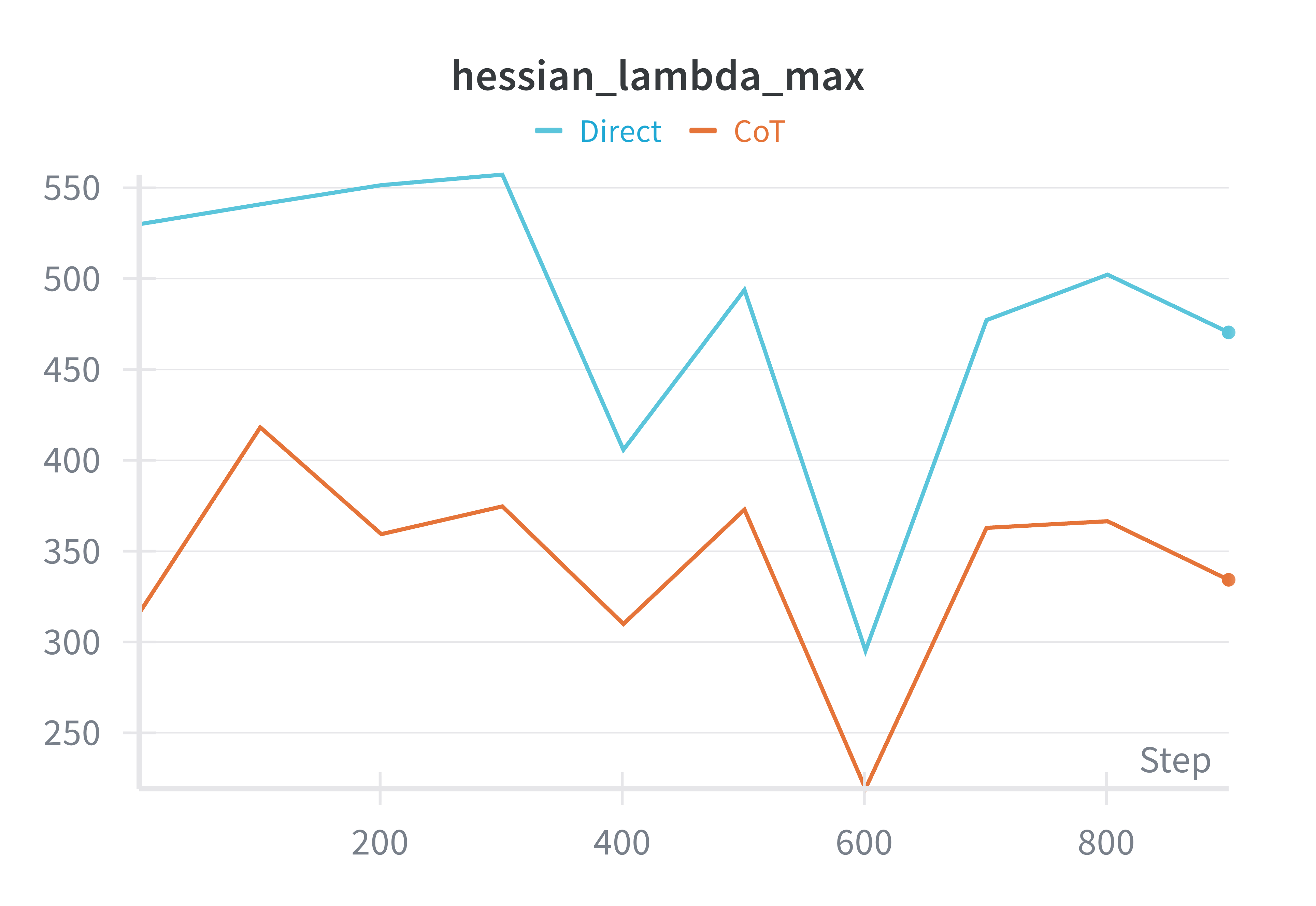
• The largest eigenvalue of the Hessian, $\lambda_{\text{max}}$​, estimated every 100 steps using the power-iteration method.

The largest eigenvalue of the Hessian, $\lambda_{\text{max}}$, serves as a practical proxy for the curvature of the loss surface: large eigenvalues indicate sharper, more unstable regions where gradients fluctuate rapidly, while smaller values correspond to flatter, better-conditioned areas that yield smoother updates and greater training stability.

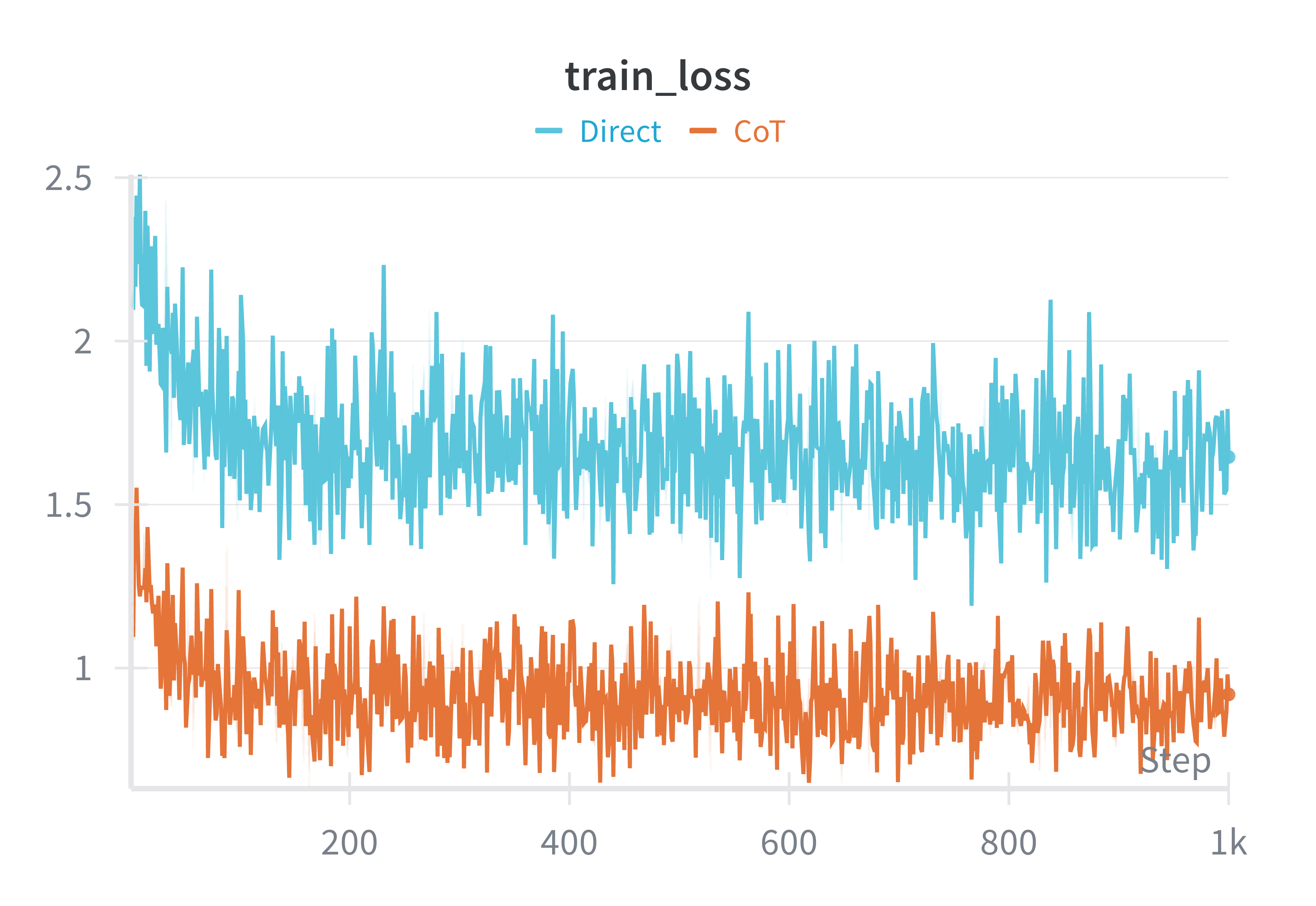
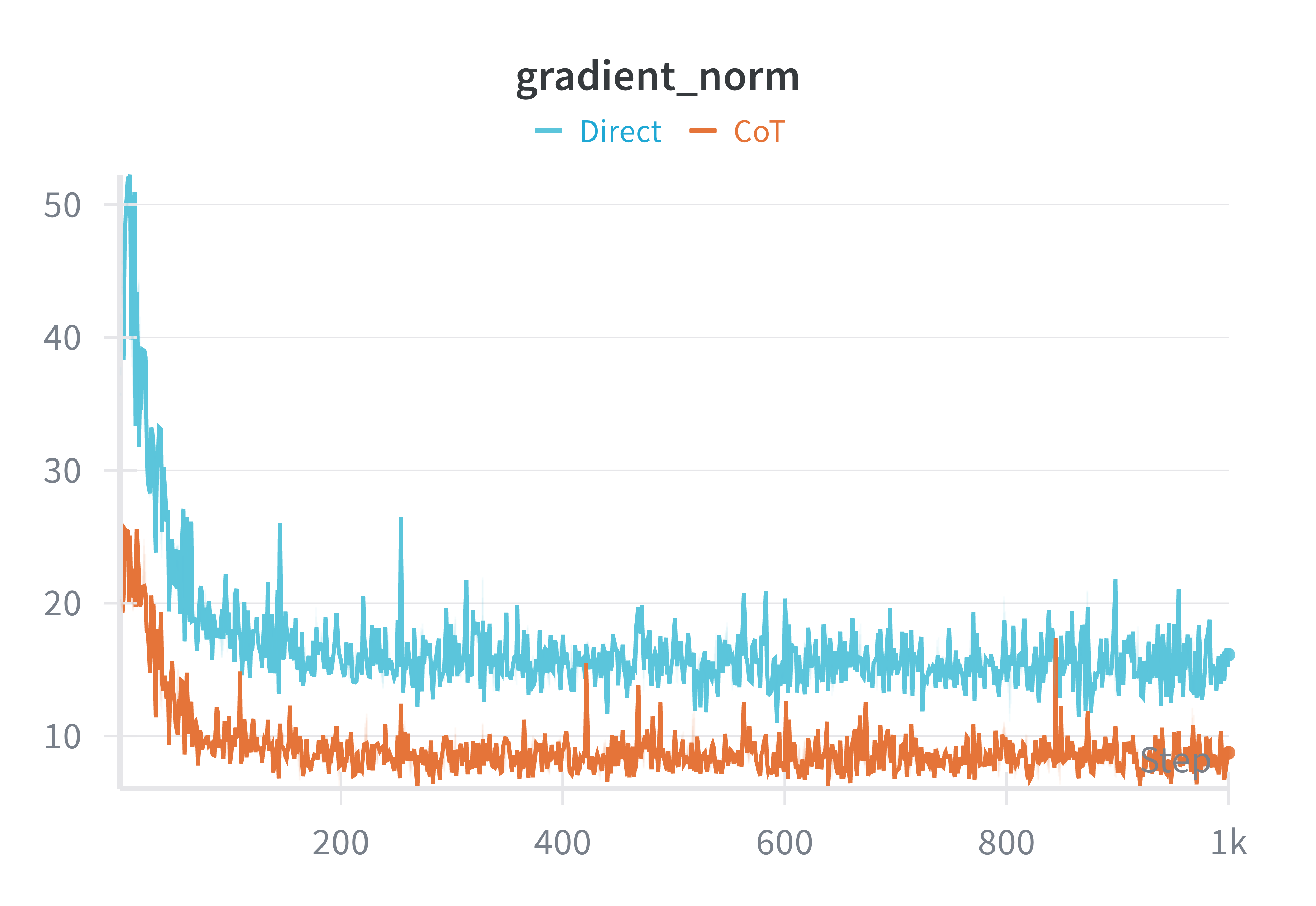
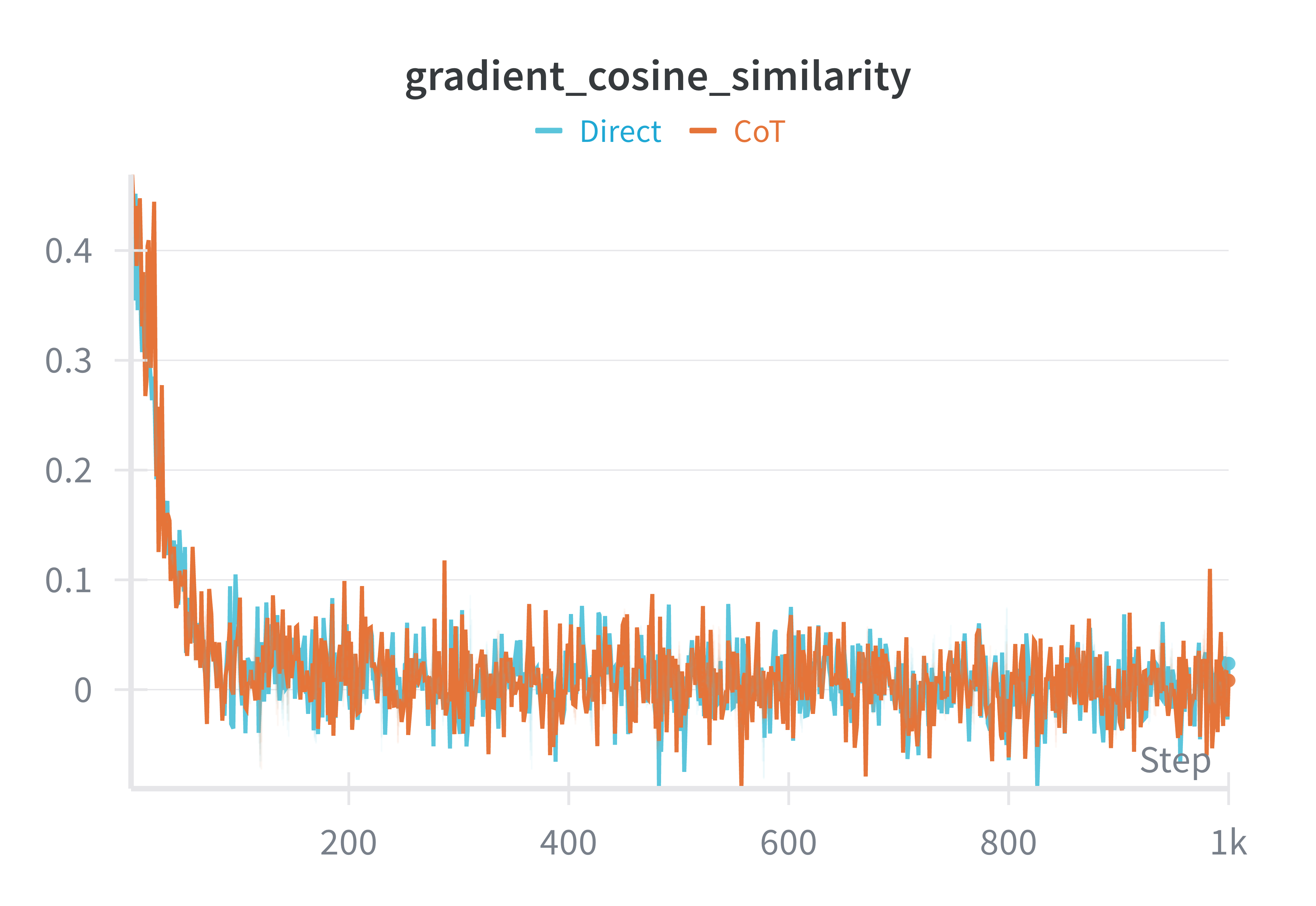
Across all runs, the training loss decreased steadily for roughly the first 150 steps before settling into a shallow oscillatory regime. This pattern is typical for low learning-rate fine-tuning on an already instruction-trained model: most of the easy loss reduction happens early. Chain-of-Thought supervision produced smaller gradient norms on average and fewer sharp spikes, suggesting that its updates were more tempered than those of direct answer-only training. The cosine similarities between consecutive gradients were broadly similar across all runs, implying that the overall direction of descent was preserved; what changed was the scale and smoothness of the steps.

The most revealing signal though came from the curvature estimates. The largest Hessian eigenvalue, $\lambda_{\max}$, was consistently lower under reasoning supervision—approximately two-thirds of the value observed in the direct, answer-only baseline. Because $\lambda_{\max}$ quantifies the steepest curvature of the loss surface, this reduction indicates that CoT training leads the model into a flatter and better-conditioned region of parameter space, something that learning rate cannot change. In such regions, small perturbations in the weights produce proportionally smaller changes in loss; optimization proceeds more predictably, and the same learning rate becomes effectively more stable. Lower curvature implies that nearby parameter configurations behave similarly: that reasoning supervision smooths not the gradients themselves, but the landscape they inhabit.

Reasoning as Implicit Alignment

For the most part, changes in logit gradients translate directly into changes in parameter gradients. The experiment above suggests that reasoning supervision affects more than the scale of these gradients: it changes the geometry of the loss surface itself. Models trained on reasoning traces converge into regions of lower curvature. This flattening implies that nearby parameter configurations yield similar loss values, so the model’s updates remain better-conditioned and less sensitive to noise. In geometric terms, reasoning supervision moves the optimizer into flatter, wider basins, where learning proceeds more stably and with smaller deviations from the original pre-trained parameters.

This behavior supports the view that reasoning supervision functions more as elicitation than just memorization. By distributing surprisal across intermediate steps of thought, Chain-of-Thought supervision regularizes the geometry of the loss landscape, improving its curvature and conditioning. The optimizer moves through flatter, better-behaved regions of parameter space, allowing updates to remain stable and directionally consistent under the same training conditions. In this regime, new reasoning patterns can be integrated without distorting the knowledge that underlies them: the model learns to refine what it already knows rather than overwrite it. Combined with the smaller gradient updates, reasoning supervision in post-training promotes less memorization and catastrophic forgetting, and guides learning toward coherence, making the parameters stay closer to the pre-trained model while aligning its behavior more closely with human-like reasoning. Philosophically, this suggests that reasoning is not merely a tool for alignment, but a natural objective for it: a way of teaching the model to think by reshaping the very geometry through which it learns.

In essence, pre-training yields a vast but rugged terrain, full of steep cliffs where token probabilities shift abruptly from one step to the next. Post-training on reasoning traces acts less like the pure addition of new knowledge, but a bit more like a smoothing operation across this surface. The same information remains, but its contours soften; gradients that once fluctuated violently begin to flow coherently along intermediate steps. The model does not merely learn new facts—it learns to traverse its own knowledge more gracefully. In the end, the gradient tells a simple story: reasoning is a way of making prediction coherent. When a model learns to smooth its own landscape—distributing complexity over time and thought—it not only mimics reasoning better, but also becomes a gentler learner.

References

[1] Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Brian Ichter, Fei Xia, Ed Chi, Quoc V. Le, and Denny Zhou. 2022. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. In Advances in Neural Information Processing Systems 35 (NeurIPS 2022).